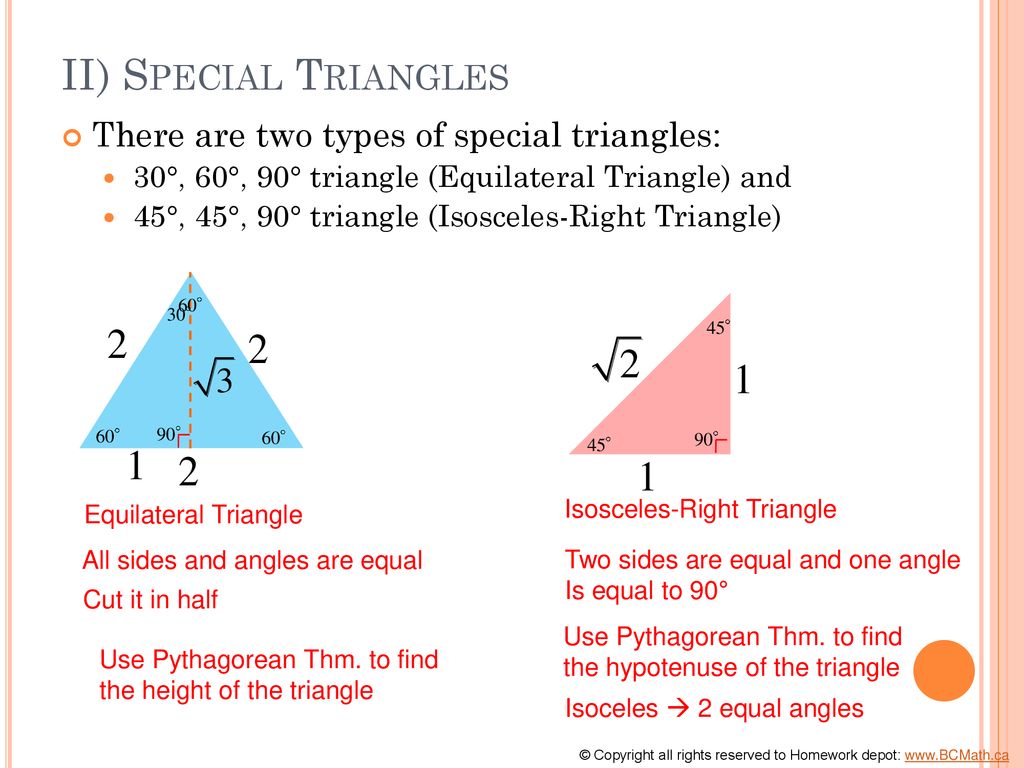
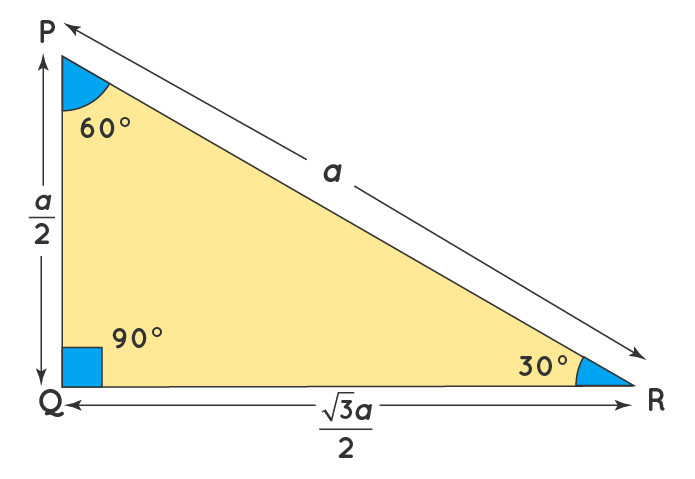
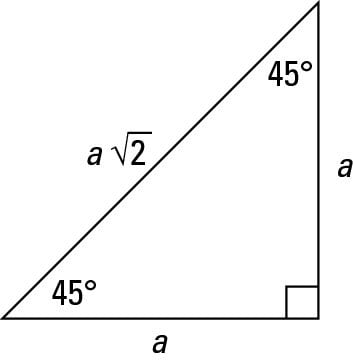
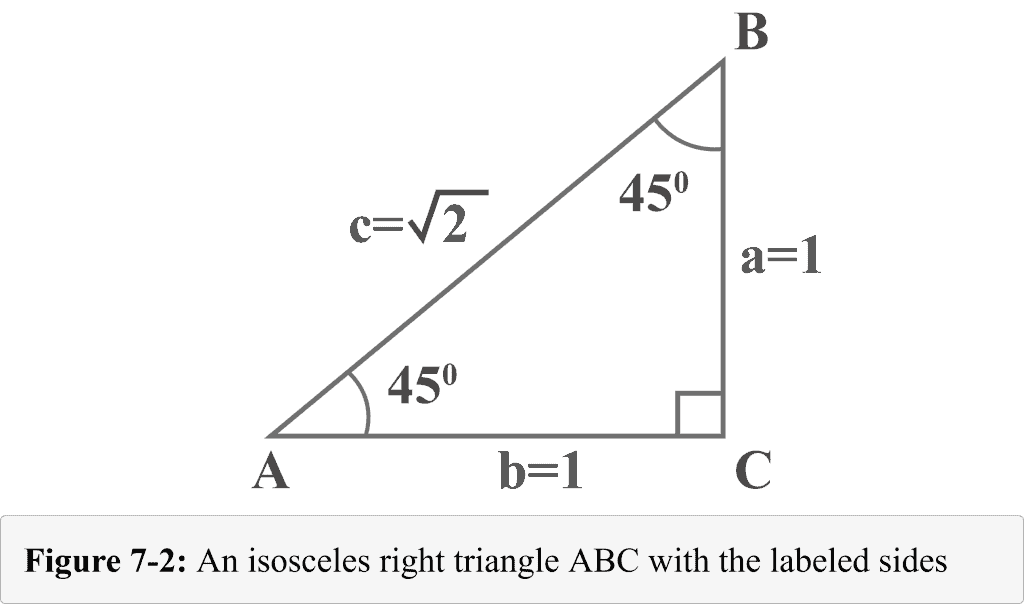
45 45 90 triangle calculator is a dedicated tool to solve this special right triangle Find out what are the sides, hypotenuse, area and perimeter of your shape and learn about 45 45 90 triangle formula, ratio and rules If you want to know more about another popular right triangles, check out this 30 60 90 triangle tool and the calculator for2 The triangle Begin with an isosceles right triangle (construct a segment, rotate it 90 degrees, connect the two remaining verticesScroll down the page for more examples and solutions on how to use the triangle The hypotenuse is always twice the length of the shorter leg (the side facing the 30° angle) The longer leg (the side facing the 60° angle) is √3 times of the shorter leg

30 60 90 Triangle
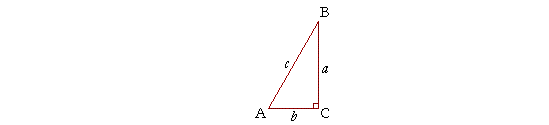
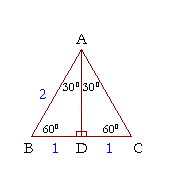
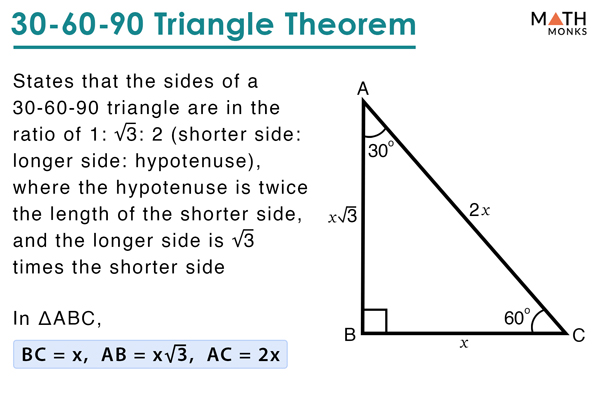
Side ratios for a 30 60 90 degree triangle
Side ratios for a 30 60 90 degree triangle-A right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, and This means that the ratio of the lengths of the shortest side to the hypotenuse of any right triangle is 12 Therefore, If a triangle is a right triangle, the ratio of the sides (short leglong leghypotenuse) is 1√32



The 30 60 90 Triangle Topics In Trigonometry
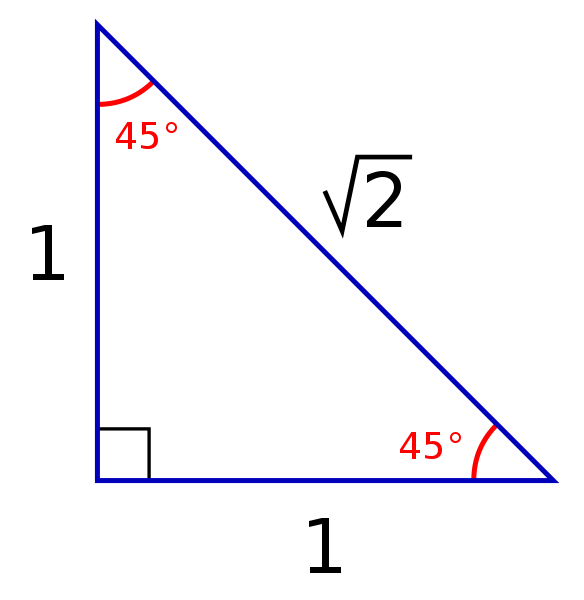
The other one is the 45 45 90 triangle These triangles are special triangles because the ratio of their sides are known to us so we can make use of this information to help us in right triangle trigonometry problems In the case of the triangle, their side's ratios are 1A triangle is one of the few special right triangles with angles and side ratios that are consistent and predictable Specifically, every triangle has a 30º angle, a 60º angle, and a 90º angle Since these angles stay the same, the ratio between the length of the sides also remains the sameIn the study of trigonometry the 30 60 90 triangle is considered a special triangle knowing the ratio of the sides of a 30 60 90 triangle allows us to find the exact values of the three trigonometric functions sine cosine and tangent for the angles 30 and 60 Special right triangles 30 60 90
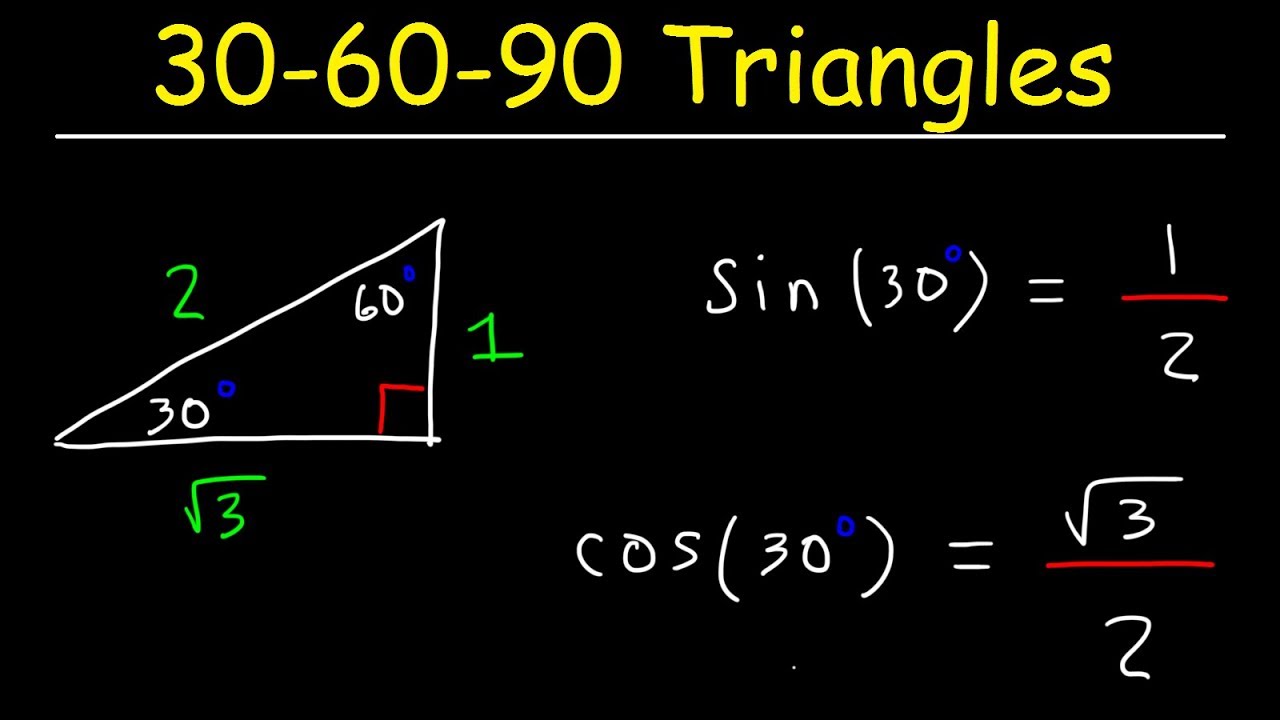
See alsoSide /angle relationships of a triangle In the figure above, as you drag the verticesof the triangle to resize it, the angles remain fixed and the sides remain in this ratio Corollary If any triangle has its sides in the ratio 1 2 √3, then it is a triangle Other triangle topics A triangle has sides that lie in a ratio 1√32 Knowing these ratios makes it easy to compute the values of the trig functions for angles of 30 degrees (π/6) and 60 degrees (π/3) Specifically sin(30) = 1/2 = 05 cos(30) = √3/2 = tan(30) = 1/√3 = sin(60) = √3/2 = cos(60) = 1/2 = 05 Prove Side Ratios for Triangle = 1sqrt (3)2
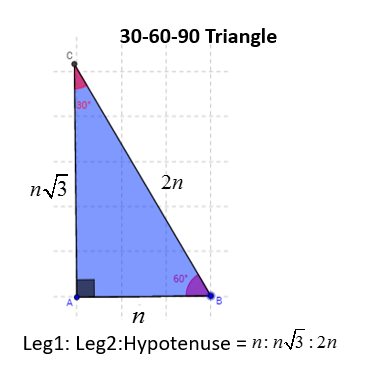
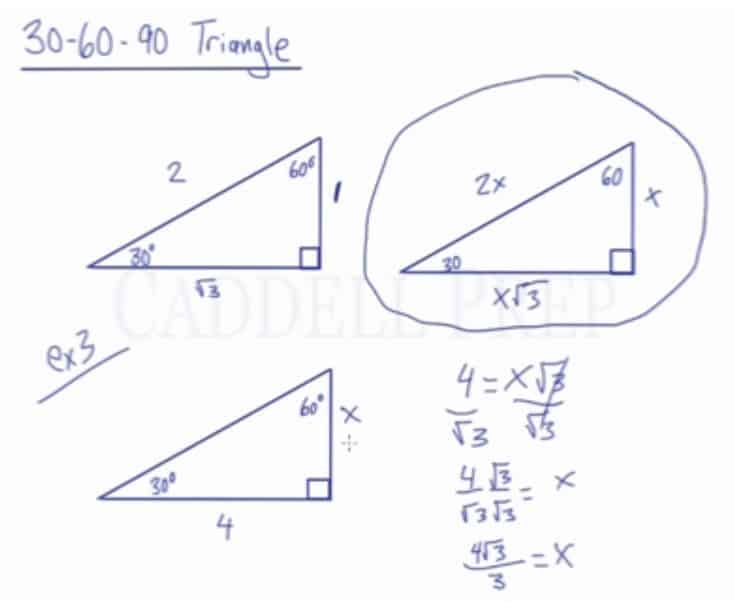
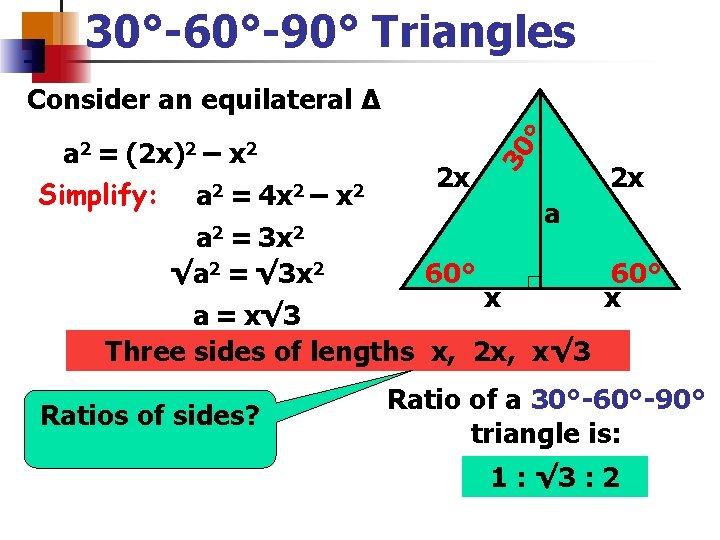
A 30 60 90 triangle completes an arithmetic progression 3030=6030 =90 An arithmetic progression is a sequence of numbers in which the difference of any two successive numbers is a constant For instance, 2,4,6,8 is an arithmetic progression with a constant of 2 Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°) Some people memorize the ratio by saying "x, 2x, x √3," because the "1, 2, 3 About Triangle A triangle is a unique right triangle whose angles are 30º, 60º, and 90º The triangle is unique because its side sizes are always in the proportion of 1 √ 32 Any triangle of the kind can be fixed without applying longstep approaches such as the Pythagorean Theorem and trigonometric features



30 60 90 Right Triangles Solutions Examples Videos



30 60 90 Triangles
Now, by construction, each half of this triangle is a triangle Q What observations can you make about the relationship between the trigonometric ratios of 30 degrees and 60 degrees? The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SATA triangle is a special right triangle that always has angles of measure 30°, 60°, and 90° All the sides of a triangle can be calculated if any one side is given



30 60 90 Triangle Explanation Examples




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation
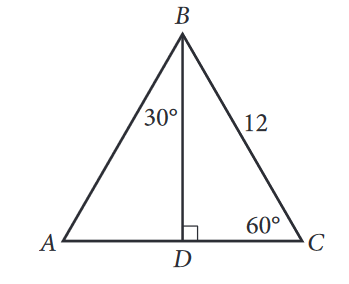
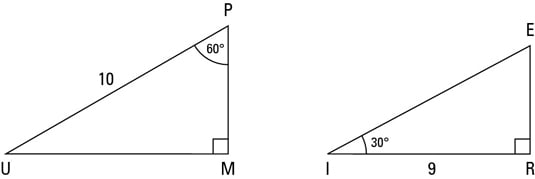
Proving the ratios between the sides of a triangleWatch the next lesson https//wwwkhanacademyorg/math/geometry/right_triangles_topic/special_rig A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in the same ratio to each otherCorrect answer Explanation We know that in a 3060=90 triangle, the smallest side corresponds to the side opposite the 30 degree angle Additionally, we know that the hypotenuse is 2 times the value of the smallest side, so in this case, that is 10 The formula for




30 60 90 Triangle Definition Math Open Reference



30 60 90 Right Triangle Side Ratios Expii
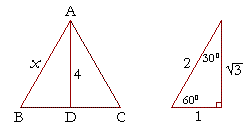
View CamScanner__1758_134jpg from MATHEMATIC 104 at University of Nairobi The ratio of the sides is then abc = 12 V52 A 300 '3 b B 600 t1 IC Principles of the 30°60°90°It is based on bisecting an equilateral triangle and using the Pythagorean theorem A 30°60°90° triangle is formed when an equilateral triangle is bisected This makes the Hypotenuse a length of x, and the short side a length of (1/2)xA triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangle




30 60 90 Triangle Calculator Formula Rules
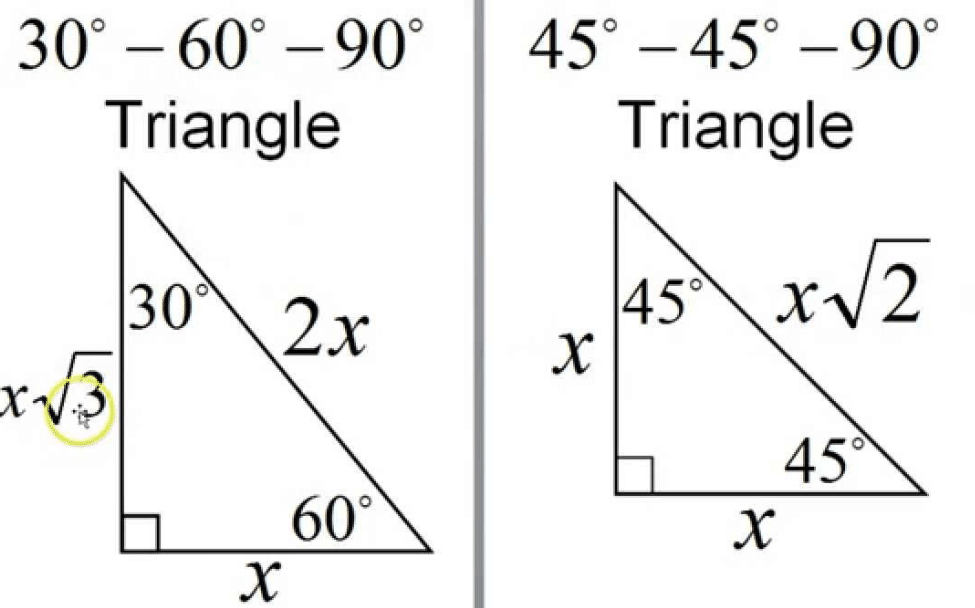



How To Work With 30 60 90 Degree Triangles Education Is Around
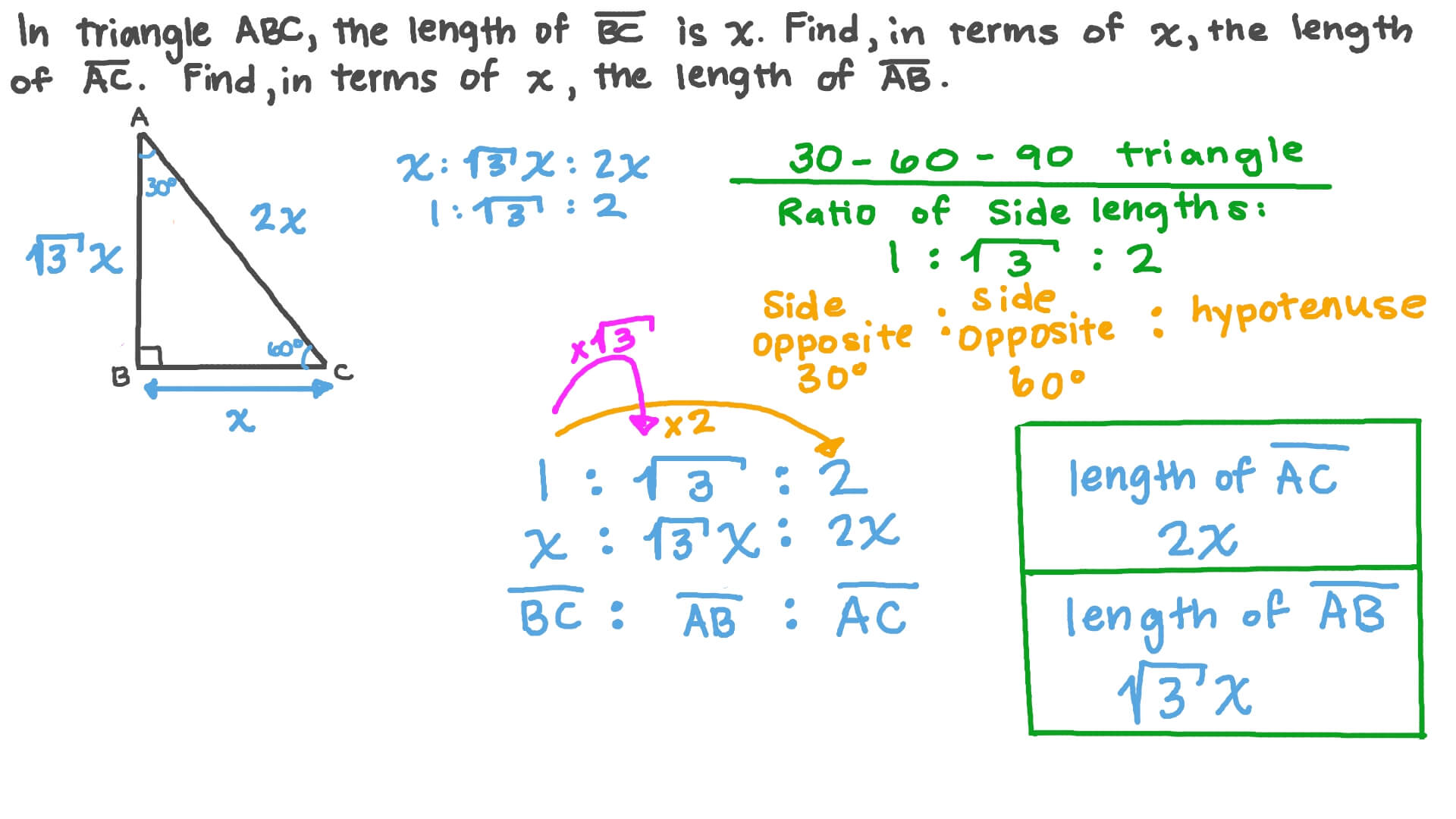
Special Triangles Isosceles and Calculator This calculator performs either of 2 items 1) If you are given a right triangle, the calculator will determine the missing 2 sides Enter the side that is known After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangleAnswer (1 of 3) If we take a triangle ABC, right angled at A And assume < B = 60°, < C = 30° Then, sin 60° = opposite side / hypotenuse => √3/2 = AC/BC = √3x / 2x & By pythagoras law, BC² = AB² AC² => BC² = x² 3x² = 4x² => BC = 2x Hence, ratio of the lengths of ABACBC = 1 √3 2While the largest side, 2, is opposite the largest angle, 90



1



1
In a triangle, the sides can be described as such Short side #1# Hypotenuse #2# Long Side #sqrt(3)# These can be considered ratios If you look at it in terms of sine and cosine, this becomes a bit clearer, since sine and cosine gives you the ratio of the sides A is a scalene triangle and each side has a different measure Since it's a right triangle, the sides touching the right angle are called the legs of the triangle, it has a long leg and a short leg, and the hypotenuse is the side across from the right angle There is a great activity for deriving the ratio of the sides of a triangle that uses an equilateral triangle with known side lengths If you draw the line that bisects one of the angles in the triangle, it is then perpendicular to the side opposite the bisected angle



30 60 90 Triangle Formulas Rules And Sides Science Trends




Which 30 60 90 Degree Triangle Is Labeled With The Correct Side Length Ratio Brainly Com
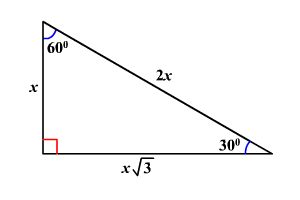
Given that the leg opposite the 30° angle for a triangle has a length of 12, find the length of the other leg and the hypotenuse The hypotenuse is 2 × 12 =These are the triangle, the 4590 triangle, and the 345 triangle THE TRIANGLE The triangle is so named because these are the sizes of its three angles The sides of this triangle are in the ratio of 1 to to 2, as shown in figure 19 10Triangle Ratio A degree triangle is a special right triangle, so it's side lengths are always consistent with each other The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




Special Right Triangles 30 60 90 Triangle Side Ratios Proof Gvlibraries Org
Start by entering the length of a triangle side Then click on which type of side it is The 5 choices you have are 30 60 90 Triangle "Short Side", "Medium Side" or "Hypotenuse" 45 45 90 Triangle "Side" or "Hypotenuse" As soon as you click that box, the output boxes will automatically get filled in by the calculatorSpecial Right Triangles Angle based Side based A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist Angle based right triangle , (Angles that form a simple ratio) Side based right triangle 345 (The lengths of the sides form a whole number ratio), approx anglesWhat I want to do in this video is discuss a special class of triangles called triangles and I think you know why they're called this the measures of its angles are 30 degrees 60 degrees and 90 degrees and what we're going to prove in this video this tends to be a very useful result at least for a lot of what you see in a geometry class and then later on in trigonometry class is the ratios between the sides of a triangle




Special Right Triangles Definition And Use The Triangle Definition There Are Many Right Angle Triangles Today We Are Most Interested In Right Ppt Download




30 60 90 Triangle
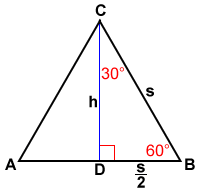
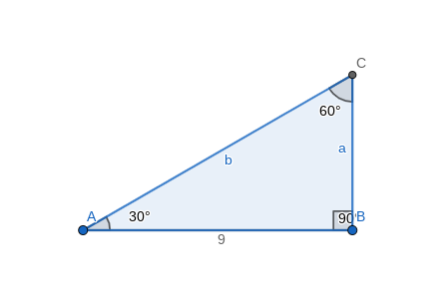
The triangle ratios {eq}cos (30)=\frac {adjacent} {hypotenuse} {/eq} {eq}cos (30)=\frac {\sqrt {3}} {2} {/eq} {eq}sin (60)=\frac {opposite} {hypotenuse} {/eq} {eq}sin (60)=\frac {\sqrt Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another The basic triangle ratio is Side opposite the 30° angle x Side opposite the 60° angle x * √ 3 Side opposite the 90° angle 2 xNow in every 30°60°90° triangle, the sides are in the ratio 1 2 , as shown on the right Whenever we know the ratios of the sides, we can solve the triangle by the method of similar figures Thus, in triangle ABC, the side corresponding to 2 has been multiplied by 5 Therefore every side will be multiplied by 5



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Side Ratios Proof Youtube
3 rows As one angle is 90, so this triangle is always a right triangle As explained above that it is Since the right angle is always the largest angle, the hypotenuse is always the longest side using property 2 We can use the Pythagorean theorem to show that the ratio of sides work with the basic triangle above a2b2=c2 12(3–√)2=13=4=c2 4–√=2=cHow are they different?



30 60 90 Triangle Rules



Question Video The Side Lengths Of 30 60 90 Triangles Nagwa
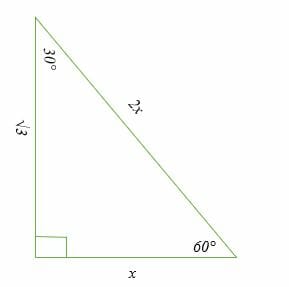
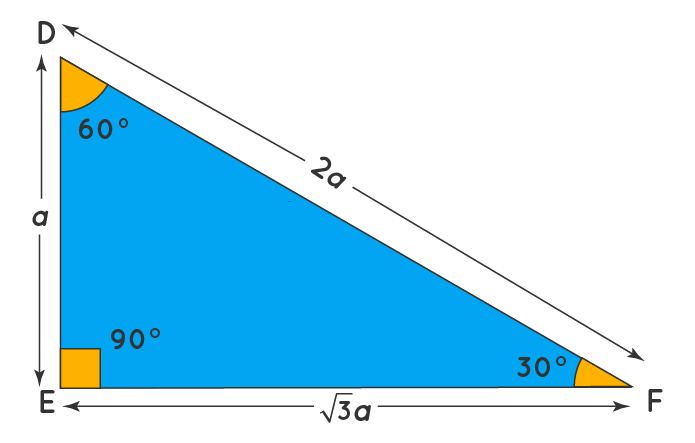
Although all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles30°60°90° Triangles There is a special relationship among the measures of the sides of a 30 ° − 60 ° − 90 ° triangle A 30 ° − 60 ° − 90 ° triangle is commonly encountered right triangle whose sides are in the proportion 1 3 2 The measures of the sides are x, x 3, and 2 xIn a 30°60°90° triangle the sides are in the ratio1 2 We will prove that below (For the definition of measuring angles by "degrees," see Topic 12) Note that the smallest side, 1, is opposite the smallest angle, 30°;




30 60 90 Right Triangle Side Ratios Expii




30 60 90 Triangle Theorem Ratio Formula Video
The 30 60 90 triangle is special because it forms an equilateral triangle when a mirror image of itself is drawn, meaning all sides are equal!A theorem in Geometry is well known The theorem states that, in a right triangle, the side opposite to 30 degree angle is half of the hypotenuse I have a proof that uses construction of equilateral triangle Is the simpler alternative proof possible using school level Geometry I want to give illustration in class roomThis allows us to find the ratio between each side of the triangle by using the Pythagorean theorem



The Complete Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Ratio Formula Video
How are the proofs for the side length ratios of and triangles similar?Specialrighttrianglesworksheetanswers 1/1 Downloaded from optimustestfreenodenet on by guest Learn shortcut ratios for the side lengths of two common right triangles 45°45°90° and 30°60°90° triangles The ratios come straight from the Pythagorean theoremThe triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 123 and the sides are in the ratio 1√3 2;



30 60 90 Triangle Formulas Rules And Sides Science Trends



Learn About The 30 60 90 Triangle Caddell Prep Online



Special Right Triangle 30 60 45 45 37 53 Elearning



30 60 90 Triangle




30 60 90 Triangles Spock S Guide To Math 4




30 60 90 Triangle Theorem Ratio Formula Video




The Side Lengths Of A 30 60 90 Triangle Are In The Ratio 1 3 2 What Is Sin 30 Brainly Com
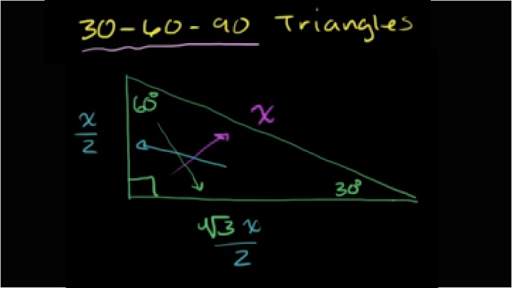



Special Right Triangles Proof Part 1 Video Khan Academy
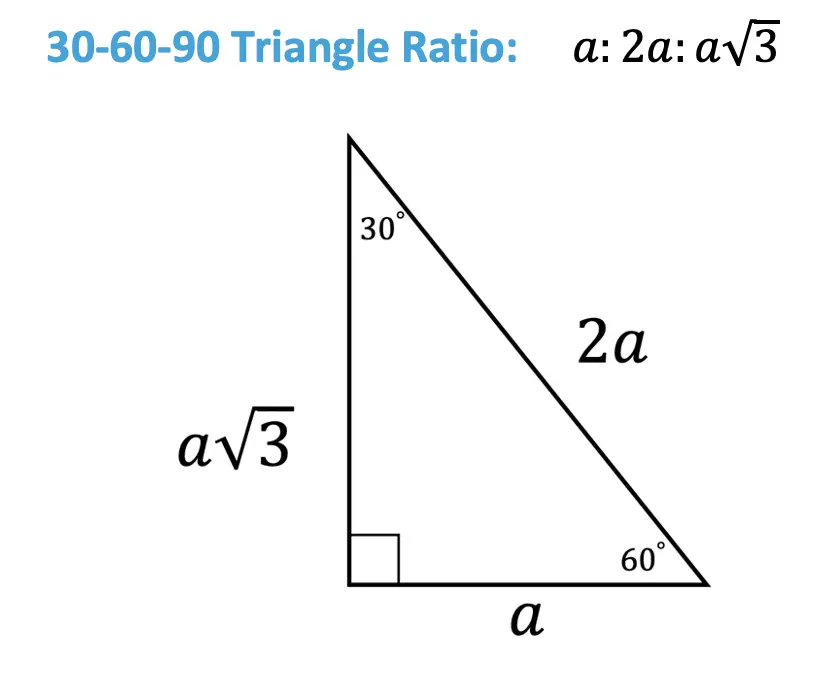



30 60 90 Special Triangles Geometry Mathsux 2
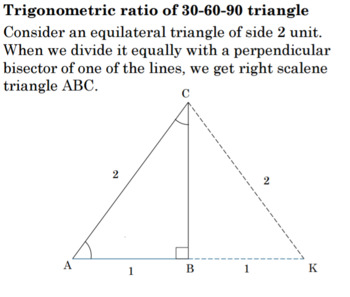



Trigonometry Of 30 60 90 Right Triangle 1 Lesson Plan G Srt C 6 Tpt




30 60 90 Triangle Theorem Ratio Formula Video




Fastest 30 60 90 Triangle Rules
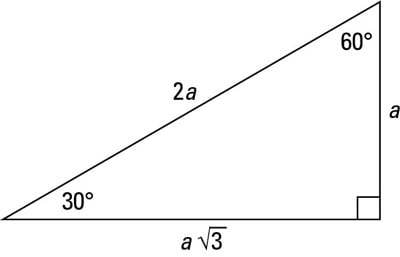



A Quick Guide To The 30 60 90 Degree Triangle Dummies



1




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com
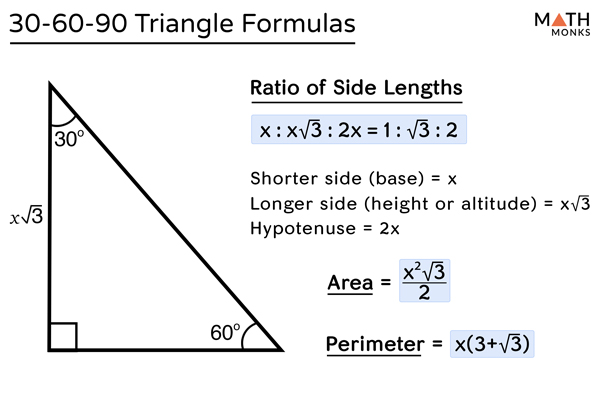



30 60 90 Triangle Definition Formulas Examples




The Side Lengths Of A 30 60 90 Triangle Are In The Ratio 1 3 2 What Is Sin 30 Brainly Com
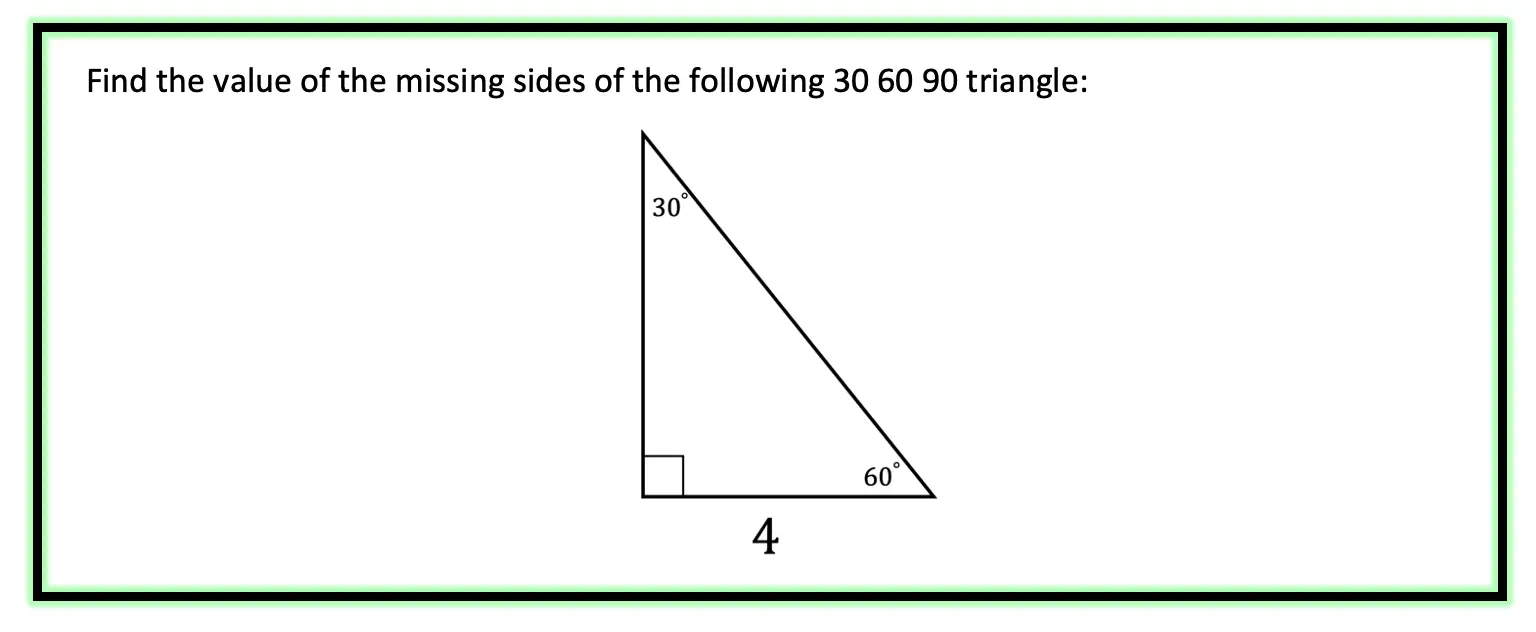



30 60 90 Special Triangles Geometry Mathsux 2




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




The 30 60 90 Triangle Topics In Trigonometry
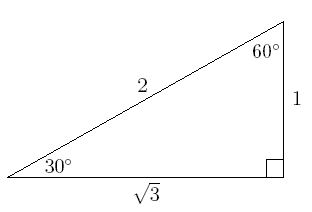



How To Use The Special Right Triangle 30 60 90 Studypug




30 60 90 Triangle Side Ratios Proof Right Triangles And Trigonometry Geometry Khan Academy Youtube
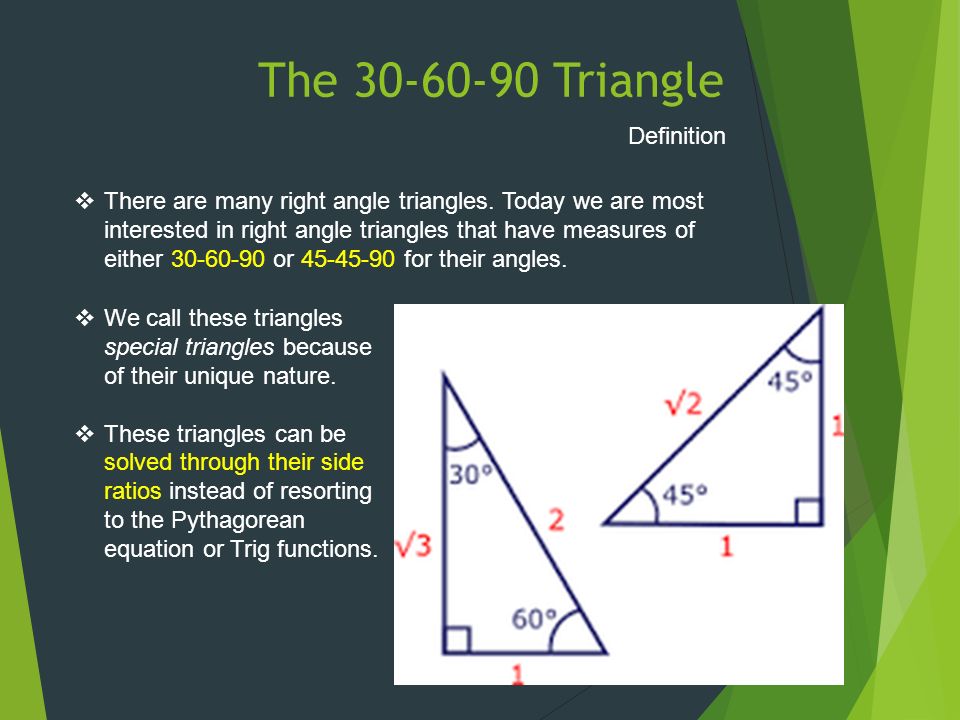



Special Right Triangles Definition And Use The Triangle Definition There Are Many Right Angle Triangles Today We Are Most Interested In Right Ppt Download
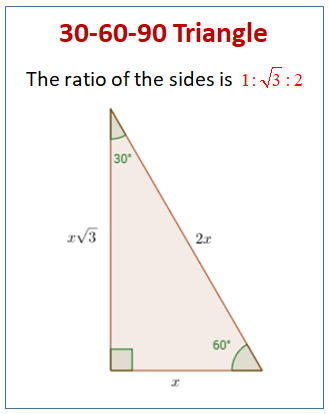



30 60 90 Special Right Triangles Videos Worksheets Examples Solutions



A 30 60 90 Triangle Math Central
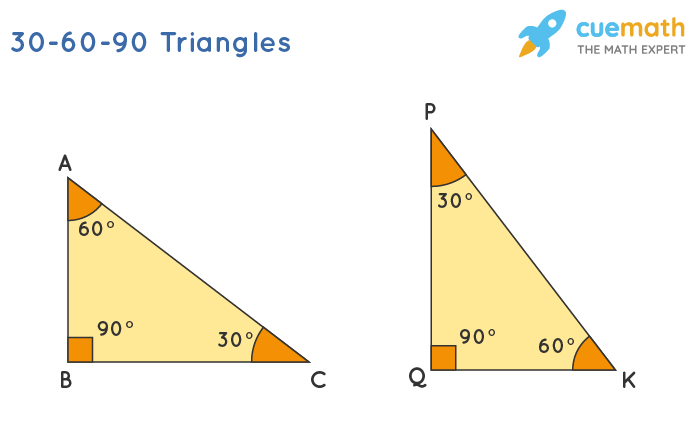



30 60 90 Triangle Definition Theorem Formula Examples
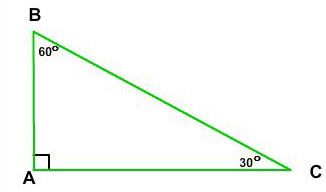



30 60 90 Right Triangle Side Ratios Expii
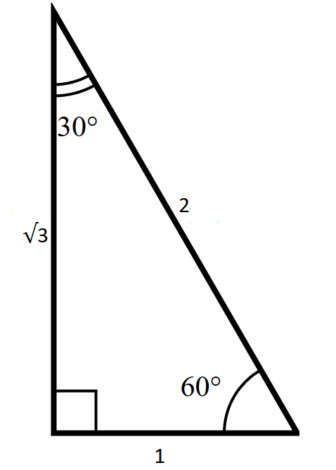



The Complete Guide To The 30 60 90 Triangle



Right Triangles With Special Angles And Side Ratios




The Side Lengths Of A 30 60 90 Triangle Are In The Ratio 1 13 2 What Is Tan 60 A Brainly Com




Special Right Triangles Part 3 30 60 90 Youtube
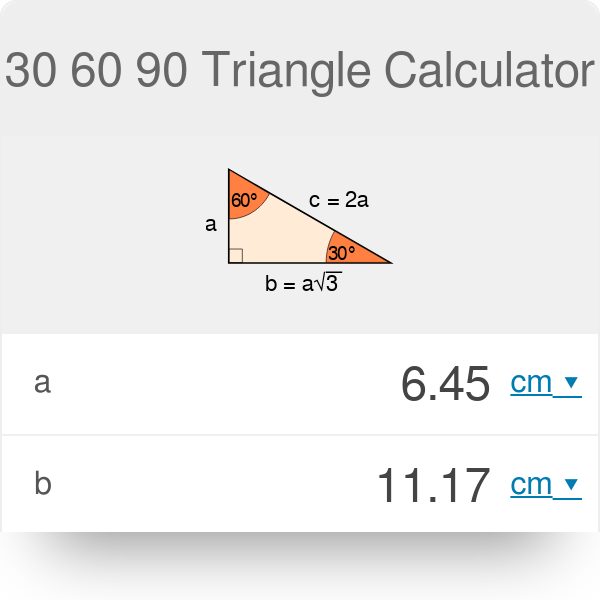



30 60 90 Triangle Calculator Formula Rules




Solved Deriving The Ratio Of The Sides Of A 30 60 90 Chegg Com




Special Right Triangles Fully Explained W 19 Examples




30 60 90 Triangle Calculator Formula Rules
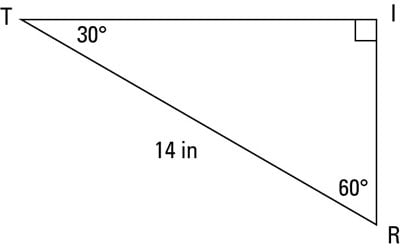



A Quick Guide To The 30 60 90 Degree Triangle Dummies



5 5 Special Triangles




Special Right Triangles




30 60 90 Triangle Explanation Examples




30 60 90 45 45 90 Special Right Triangles Youtube




30 60 90 Triangle Theorem Ratio Formula Video



The Easy Guide To The 30 60 90 Triangle



Special Right Triangles Activity Builder By Desmos
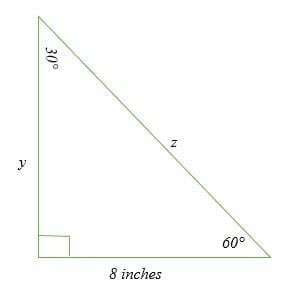



30 60 90 Triangle Explanation Examples
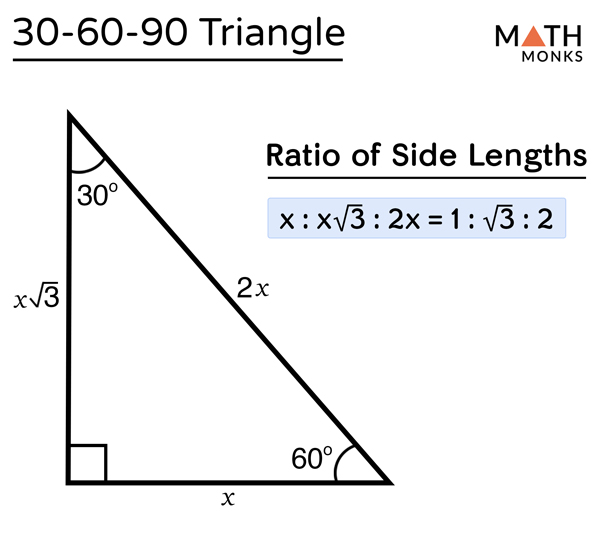



30 60 90 Triangle Definition Formulas Examples



Section 2 2 Trig Ratios With Any Angle Ppt Download



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Theorem Ratio Formula Video



What Are The Side Ratios For A 30 60 90 Triangle Quora
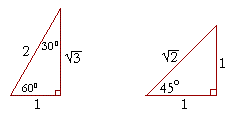



The 30 60 90 Triangle Topics In Trigonometry



The Easy Guide To The 30 60 90 Triangle




File 30 60 90 Triangle Svg Wikimedia Commons




30 60 90 Right Triangles Free Math Help



How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies



We Make A Living By What We Get



The 30 60 90 Triangle Topics In Trigonometry



30 60 90 Triangle Definition Theorem Formula Examples



Special Angles In Trigonometry




Instructions Use The Ratio Of A 30 60 90 Triangle To Solve For The Variables Leave Your Answers As Brainly Com



The Easy Guide To The 30 60 90 Triangle



Identifying The 30 60 90 Degree Triangle Dummies



What Are Some Differences And Similarities Between 30 60 90 Triangles And 45 45 90 Triangle Quora



30 60 90 Triangle Definition Theorem Formula Examples



30 60 90 Triangles Special Right Triangle Trigonometry Youtube




Day 1 Hw Special Right Triangles 45 45 90 30 60 90 Youtube Trigonometry Worksheets Right Triangle Triangle Worksheet



What Are The Side Ratios For A 30 60 90 Triangle Quora



Tarantamath Licensed For Non Commercial Use Only Razan 10 3




Hints For Problem 5 To Find The Height Of An Chegg Com



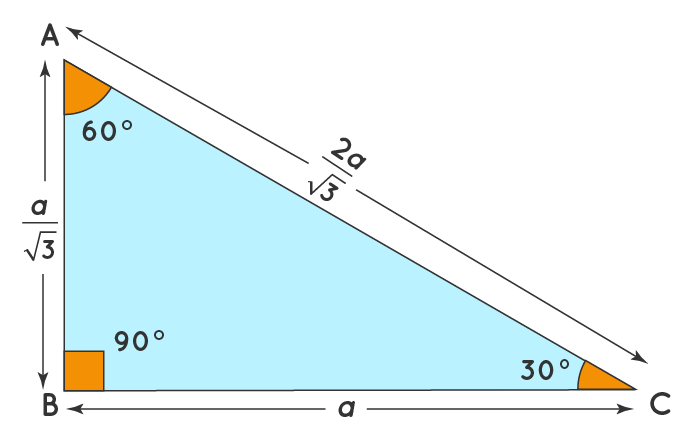
Activity 22 Construct A 30 60 90 Triangle Geogebra




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




How To Find The Area Of A Regular Polygon Using Special Right Triangles Geometry Study Com




30 60 90 Triangles Hd Youtube



The Easy Guide To The 30 60 90 Triangle




Pythagorean Theorem Review 5 Questions If A Triangle




Solved Question 6 What Is The Ratio Of The Side Lengths Of A Chegg Com



1




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com



A 30 60 90 Triangle



30 60 90 Triangle Definition Formulas Examples



0 件のコメント:
コメントを投稿